공간좌표에서의 일차방정식

• 공간좌표는 x,y,z 세 좌표가 존재하는 좌표를 말한다.

공간좌표에선....

• 평면을 결정짓기 위해 최소 세 개의 점이 필요하다.
• ax+ by + cz = n  일차방정식으로 평면을 표현할 수 있다.
• 하나의 일차방정식에서 미지수 중 하나의 값을 특정 상수로 제한시키는 식으로 직선을 표현할 수 있지만, xy평면 / yz평면 / zx평면에 평행한 직선만 제한적으로 표현 가능하다.
• 서로 평행하지 않은 두 평면의 교차지점 = 직선이므로, 평면을 표현하는 일차방정식 두 개로 직선을 표현할 수 있다.

xy평면 : z좌표값 = 0

yz평면 : x좌표값 = 0

zx평면 : y좌표값 = 0

---

<공간상에서 평면을 나타내는 일차방정식>

아래와 같은 일차방정식은 공간상에서 평면을 나타낸다. 

 

평면의 방정식
: ax+ by + cz = n 
(단, 모든 미지수의 계수가 0인 상황 즉 미지수가 없는 상황은 제외)

 

아래 x = 6 (파란색 평면) 처럼 단 하나라도 미지수가 있으면 공간상에서는 평면으로 정의된다는 점에 유의. 

(단, 만약 x = 6 (z = 3) 과 같이 나머지 미지수들 중 하나라도 값이 별도로 정확히 정의된다면 직선이 된다.)

공간좌표상에서 나타나는 평면들

xy평면상에서 본 것. 붉은 평면이 직사각형 형태로 넓게 보이는 것은 절대로 xy평면 상에서 해에 해당하는 부분이 저만큼이라서가 아니다. xy평면과 붉은 평면은 단 하나의 직선상에서만 만나고 나머지는 xy평면 위로 솟은 부분이다.

• 빨간색 평면(x+y+z=7): 전형적인 공간좌표에서의 평면. xy평면과 겹치는 부분은 z=0을 대입한 식의 방정식인 x+y=7 (z=0) 이다.
• 노란색 평면(x+y=9): xy평면상에서 전형적인 방정식 직선 형태를 보이는데, z좌표 값이 정의되지 않았기 때문에 xy평면상에서 보이는 직선이 그대로 z축 방향으로만 확장된 형태의 평면으로 나타나진다.
• 파란색 평면(x=6): y좌표 값이 정의되어있지 않아, xy평면에서는 x=6에서 세로로 일직선인 형태를 나타냄. 공간좌표에서는 z좌표 값 또한 정의되어있지 않은 점이 반영되어, xy좌표상에서 나타나는 일직선에서 그대로 높이만 확장된 형태의 평면.

---

<공간상에서 직선을 나타내는 일차방정식(1) - 제한적 >

앞서 공간상에서 직선을 표현하려고 'x+y=7 (z=0)' 과 같은 방식으로 쓴 것을 보면 알겠지만, 기존의 일차방정식으로는 공간상에서 직선을 정의하는데 한계가 있다. 좌표평면에서는 기울기와 한 점으로 직선을 표현하는데, 공간상에서는 이와 같은 방식으로 표현할 수 있는 직선은 xy평면, yz평면, zx평면과 평행한 직선뿐이기 때문이다.

 

더 자세히 적어보자면...

 

직선은 서로 다른 두 점으로 결정할 수 있는 존재이다. 이것은 평면상에서도 공간상에서도 동일하다.

평면상에서는 직선을 정의할때 기울기와 한 점으로 정의한다.

  좌표평면에서 기울기의 정의

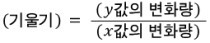
그러나 공간상에는 x,y,z 총 세 개의 좌표가 존재하기 때문에, 단 두 개의 미지수 변화량으로만 계산하며 나머지 한 미지수는 논외가 되는 이 '기울기'라는 개념을 적용하기가 굉장히 곤란하다.

굳이 이 '기울기'라는 개념으로 공간상의 직선을 표현해보자면, 나머지 한 미지수는 상수값을 고정시키는 식으로 xy평면, yz평면, zx평면과 평행한 직선은 표현할 수 있겠다. (가령, 'x+y=-3 (z=4)' 와 같은 방식으로 적으면 xy평면과 평행한 직선을 표현할 수 있다)

---

<공간상에서 직선을 나타내는 일차방정식(2)>

 

사진의 (a)와 같이 '서로 평행하지 않은 두 평면의 교차지점(intersection line) = 직선'인 점에서 착안하여, 평면을 표현하는 일차방정식 두 개로 공간상에서 직선을 표현할 수 있다.

​3D 공간에서 직선은 한 개의 방정식으로 표현될 수 없다. 이것의 이유는 공간은 3차원인데 반해 직선은 1차원이기 때문이다.(*평면은 2차원이고 직선은 1차원임.) 3차원 공간에서 선을 결정지으려면 두 차원을 날려버려야한다. 이것을 위해 우리는 두 방정식이 필요함: 각자의 추가 차원을 날리는 방정식들.

아주 조금 덜 추상적으로 말하자면, R^3(3차원)에서 직선은 단지 두 평면의 교차지점일뿐이다.

 

... 구체적인 예시로서, 두 평면 x=0 그리고 y=0 의 교차지점은 z축이다.

 

 

 

https://math.stackexchange.com/questions/1026710/what-is-the-equation-for-a-straight-line-in-a-3d-space-and-how-to-find-other-pa

What is the Equation for a straight line in a 3D space? And how to find other parelell lines to it?